Niget: NanoIndentation General Evaluation Tool References

Appendix A Data fitting

We use types of data fitting: the Deming fit for straight lines, the least squares fit of the 3/2 power and orthogonal distance regression [2] for power law functions.

A.1 Orthogonal distance regression

Orthogonal distance regression, also called generalized least squares regression, errors-in-variables models or measurement error models, attempts to tries to find the best fit taking into account errors in both x- and y- values. Assuming the relationship

$y^{*}=f(x^{*};\beta)$

(60)

where $\beta$ are parameters and $x^{*}$ and $y^{*}$ are the “true” values, without error, this leads to a minimization of the sum

$\min_{\beta,\delta}\sum_{i=1}^{n}\left[\left(y_{i}-f(x_{i}+\delta;\beta)\right% )^{2}+\delta_{i}^{2}\right]$

(61)

which can be interpreted as the sum of orthogonal distances from the data points $(x_{i},y_{i})$ to the curve $y=f(x,\beta)$ . It can be rewritten as

$\min_{\beta,\delta,\varepsilon}\sum_{i=1}^{n}\left[\varepsilon_{i}^{2}+\delta_% {i}^{2}\right]$

(62)

subject to

$y_{i}+\varepsilon_{i}=f(x_{i}+\delta_{i};\beta).$

(63)

This can be generalized to accomodate different weights for the datapoints and to higher dimensions

$\min_{\beta,\delta,\varepsilon}\sum_{i=1}^{n}\left[\varepsilon_{i}^{T}w^{2}_{% \varepsilon}\varepsilon_{i}+\delta_{i}^{T}w^{2}_{\delta}\delta_{i}\right],$

where $\varepsilon$ and $\delta$ are and dimensional vectors and $w_{\varepsilon}$ and $w_{\delta}$ are symmetric, positive diagonal matrices. Usually the inverse uncertainties of the data points are chosen as weights. We use the implementation ODRPACK [2].

There are different estimates of the covariance matrix of the fitted parameters $\beta$ . Most of them are based on the linearization method which assumes that the nonlinear function can be adequately approximated at the solution by a linear model. Here, we use an approximation where the covariance matrix associated with the parameter estimates is based $\left(J^{T}J\right)^{-1}$ , where is the Jacobian matrix of the x and y residuals, weighted by the triangular matrix of the Cholesky factorization of the covariance matrix associated with the experimental data. ODRPACK uses the following implementation [1]

$\hat{V}=\hat{\sigma}^{2}\left[\sum_{i=1}^{n}\frac{\partial f(x_{i}+\delta_{i};% \beta)}{\partial\beta^{T}}w^{2}_{\varepsilon_{i}}\frac{\partial f(x_{i}+\delta% _{i};\beta)}{\partial\beta}+\frac{\partial f(x_{i}+\delta_{i};\beta)}{\partial% \delta^{T}}w^{2}_{\delta_{i}}\frac{\partial f(x_{i}+\delta_{i};\beta)}{% \partial\delta}\right]$

(64)

The residual variance $\hat{\sigma}^{2}$ is estimated as

$\hat{\sigma}^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left[\left(y_{i}-f(x_{i}+\delta;% \beta)\right)^{T}w^{2}_{\varepsilon_{i}}\left(y_{i}-f(x_{i}+\delta;\beta)% \right)+\delta_{i}^{T}w^{2}_{\delta_{i}}\delta_{i}\right]$

(65)

where $\beta\in\mathbb{R}^{p}$ and $\delta_{i}\in\mathbb{R}^{m},\ i=1,\dots,n$ are the optimized parameters,

A.2 Total least squares - Deming fit

The Deming fit is a special case of orthogonal regression which can be solved analytically. It seeks the best fit to a linear relationship between the x- and y-values

$y^{*}=ax^{*}+b,$

(66)

by minimizing the weighted sum of (orthogonal) distances of datapoints from the curve

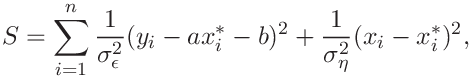$S=\sum_{i=1}^{n}\frac{1}{\sigma_{\epsilon}^{2}}(y_{i}-ax_{i}^{*}-b)^{2}+\frac{% 1}{\sigma_{\eta}^{2}}(x_{i}-x_{i}^{*})^{2},$

with respect to the parameters , , and $x_{i}^{*}$ . The weights are the variances of the errors in the x-variable ( $\sigma_{\eta}^{2}$ ) and the y-variable ( $\sigma_{\epsilon}^{2}$ ). It is not necessary to know the variances themselves, it is sufficient to know their ratio

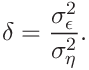$\delta=\frac{\sigma_{\epsilon}^{2}}{\sigma_{\eta}^{2}}.$

(67)

The solution is

$\displaystyle a$	$\displaystyle=$	$\displaystyle\frac{1}{2s_{xy}}\left[s_{yy}-\delta s_{xx}\pm\sqrt{(s_{yy}-% \delta s_{xx})^{2}+4\delta s_{xy}^{2}}\right]$	(68)
$\displaystyle b$	$\displaystyle=$	$\displaystyle\bar{y}-a\bar{x}$	(69)
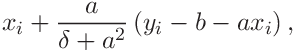$\displaystyle x_{i}^{*}$	$\displaystyle=$	$\displaystyle\ x_{i}+\frac{a}{\delta+a^{2}}\left(y_{i}-b-ax_{i}\right),$	(70)

where

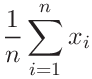$\displaystyle\bar{x}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}x_{i}$	(71)
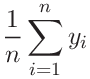$\displaystyle\bar{y}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}y_{i}$	(72)
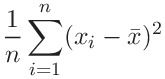$\displaystyle s_{xx}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}$	(73)
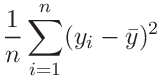$\displaystyle s_{yy}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}$	(74)
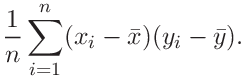$\displaystyle s_{xy}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y}).$	(75)

A.3 Least squares - 3/2 power fit

We seek the best fit

$y=ax^{3/2}+b,$

(76)

by minimizing the sum of (vertical) distances of datapoints from the curve

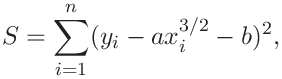$S=\sum_{i=1}^{n}(y_{i}-ax_{i}^{3/2}-b)^{2},$

with respect to the parameters , . The solution is

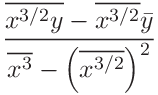	$\displaystyle a$	$\displaystyle=$	$\displaystyle\frac{\overline{x^{3/2}y}-\overline{x^{3/2}}\bar{y}}{\overline{x^% {3}}-\left(\overline{x^{3/2}}\right)^{2}}$		(77)
	$\displaystyle b$	$\displaystyle=$	$\displaystyle\bar{y}-a\overline{x^{3/2}}$		(78)

where

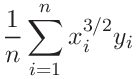$\displaystyle\overline{x^{3/2}y}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}x_{i}^{3/2}y_{i}$	(79)
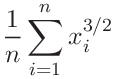$\displaystyle\overline{x^{3/2}}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}x_{i}^{3/2}$	(80)
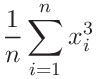$\displaystyle\overline{x^{3}}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}x_{i}^{3}$	(81)
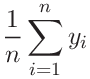$\displaystyle\bar{y}$	$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{i=1}^{n}y_{i}$	(82)

References References

Generated on Mon Nov 19 13:56:12 2018 by LaTeXML [LOGO]